这篇文章是Tensorflow系列文章中的第三篇，还是比较基础，主要想细致记录和总结一下Tensorflow中常用的损失函数。主要参考但不限于书籍Nick McClure的 Tensorflow Machine Learning Cookbook 中文版《Tensorflow机器学习实战指南》。文中涉及到的代码的完整源码都放在了Github里MachineLearningNotes–Tensorflow当中了。

Tensorflow中常用损失函数

前面这几种(1~3)主要讲解回归算法的损失函数，预测连续因变量。在回归算法中常用的损失函数表述前提，都是针对创建的张量，预测序列 x_vals 和 目标序列 target 的：

x_vals = tf.linspace(-1., 1., 500)
target = tf.constant(0.)

1.L2正则损失函数(欧拉损失函数)

l2_y_vals = tf.square(target - x_vals)
l2_y_out = sess.run(l2_y_vals)
# same as (t1-x1)^2 + .... +(tn-xn)^2
# Tensorflow内建L2正则形式，nn.l2_loss() = 1/2 * l2_y_vals
print('- - - - - - - -l2_y_vals - - - - - - - - - -')
print(l2_y_out)

L2正则损失函数，是预测值和目标值差值的平方和。实现的功能类似以下公式 ：

L2正则损失函数是非常有用的损失函数，因为它在目标值附近有更好的曲度，机器学习利用这一点进行收敛，离目标越近收敛越慢。
同时，Tensorflow 中有内建 l2正则损失函数: tf.nn.l2_loss() 效果类似上述 1/2 * l2_y_vals。
还有一个 tf.losses.mean_squared_error(target, x_vals) 的方法与 L2 正则损失函数较为类似，它是求平方根误差。
输出的 l2_y_out 如下：

- - - - - - - -l2_y_vals - - - - - - - - - -
[1.00000000e+00 9.92000103e-01 9.84032154e-01 9.76096511e-01
 ......
 1.17433242e-01 1.14702344e-01 1.12003572e-01 1.09336890e-01
 1.06702380e-01 1.04099996e-01 1.01529695e-01 9.89915729e-02
 ......
 1.39798662e-02 1.30481338e-02 1.21485433e-02 1.12810815e-02
 1.04457354e-02 9.64253023e-03 8.87145288e-03 8.13249312e-03
 7.42567237e-03 6.75097015e-03 6.10840600e-03 5.49797015e-03
 4.91965376e-03 4.37347405e-03 3.85942264e-03 3.37749231e-03
 2.92769750e-03 2.51003075e-03 2.12448649e-03 1.77107635e-03
 1.44979416e-03 1.16063596e-03 9.03610373e-04 6.78712793e-04
 4.85940691e-04 3.25299741e-04 1.96786816e-04 1.00400750e-04
 3.61444145e-05 4.01588659e-06 4.01612579e-06 3.61451312e-05
 1.00400750e-04 1.96786816e-04 3.25301895e-04 4.85940691e-04
 6.78712793e-04 9.03613924e-04 1.16063596e-03 1.44979416e-03
 1.77108136e-03 2.12448649e-03 2.51003075e-03 2.92770402e-03
 3.37749231e-03 3.85942264e-03 4.37348196e-03 4.91965376e-03
 5.49797015e-03 6.10841531e-03 6.75097015e-03 7.42567237e-03
 8.13250430e-03 8.87144171e-03 9.64253023e-03 1.04457475e-02
 ......
 8.91603008e-02 9.15699527e-02 9.40116569e-02 9.64855701e-02
 9.89916101e-02 1.01529695e-01 1.04099996e-01 1.06702417e-01
 ......
 9.44674850e-01 9.52482104e-01 9.60321546e-01 9.68193054e-01
 9.76096511e-01 9.84032273e-01 9.92000222e-01 1.00000000e+00]

2.L1正则损失函数(绝对值损失函数)

l1_y_vals = tf.abs(target - x_vals)
l1_y_out = sess.run(l1_y_vals)
# same as |t1-x1| + .... +|tn-xn|

L1正则损失函数是预测值和目标值差值的绝对值之和，实现的功能类似以下公式 ：

L1正则损失函数在绝对值附近不平滑，直接使用算法不能很好地收敛。
同样，也有一个 tf.losses.absolute_difference 方法 与 L1正则损失函数 功能类似。

3.Pseudo-Huber 损失函数

delta1 = tf.constant(0.25)  
phuber1_y_vals = tf.multiply(tf.square(delta1), tf.sqrt(1. + tf.square((target - x_vals)/delta1)) - 1.)
phuber1_y_out = sess.run(phuber1_y_vals)  

delta2 = tf.constant(5.)  
phuber2_y_vals = tf.multiply(tf.square(delta2), tf.sqrt(1. + tf.square((target - x_vals)/delta2)) - 1.)
phuber2_y_out = sess.run(phuber2_y_vals)

Pseudo-Huber 损失函数是 Huber损失函数的连续平滑估计，试图使用 L1 和 L2 正则削减极值处的陡峭，使损失函数在目标值附近连续。Pseudo-Huber 损失函数的表达式依赖参数 delta。实现的功能类似以下公式 ：

---

针对以下在分类算法中常用的损失函数，重新给 x_vals 和 target 进行赋值：

x_vals = tf.linspace(-3., 5., 500)  
target = tf.constant(1.)
targets = tf.fill([500,], 1.)

4.Hinge损失函数

hinge_y_vals = tf.maximum(0., 1. - tf.multiply(target, x_vals))
hinge_y_out = sess.run(hinge_y_vals)  
# 上述算法使目标值为1，预测值距离1越近，损失函数值越小

Hinge损失函数主要用来评估支持向量机算法。本例计算两个目标类之间的损失，使用目标值为1时，预测值距离1越近，损失函数值越小。
实现的功能类似以下公式 ：

5.Cross-entropy loss 两类交叉熵损失函数(逻辑损失函数)

xentropy_y_vals = - tf.multiply(target, tf.log(x_vals)) - tf.multiply((1. - target), tf.log(1. - x_vals))  
xentropy_y_out = sess.run(xentropy_y_vals)  
# same as -(t * log(x)) - [(1 - t) * log(1 - x)]  
# -\left [ t * log\left ( x \right ) \right ] - \left [ \left ( 1 - t \right ) * log\left ( 1-x \right ) \right ]

Cross-entropy loss 两类交叉熵损失函数 主要用于使用信息论中的交叉熵的理论， 度量预测值到真实值的距离。例如预测两类目标 0 或者 1 时，希望知道预测值和真实分类值之间的实数距离，可以使用逻辑损失函数。
实现的功能类似以下公式 ：

6.Sigmoid交叉熵损失函数

xentropy_sigmoid_vals = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_vals, labels=targets)
xentropy_sigmoid_out = sess.run(xentropy_sigmoid_vals)
# 先将x_vals值通过sigmoid函数转换,再计算交叉熵损失

Sigmoid交叉熵损失函数 与 上述逻辑损失函数的区别是，先将x_vals值通过sigmoid函数转换，再计算 x_vals 与 targets 的交叉熵损失
注意新版本的 Tensorflow 的 tf.nn.sigmoid_cross_entropy_with_logits 方法 需要传入 logits 和 labels，参考代码时需要注意。
之所以这里使用 targets, 是因为 logits 和 labels 必须具有相同的type和shape。
公式近似如下：

7.加权交叉熵损失函数(Weighted cross entropy loss)

weight = tf.constant(0.5)  
xentropy_weighted_y_vals = tf.nn.weighted_cross_entropy_with_logits(targets, x_vals, weight)  
xentropy_weighted_y_out = sess.run(xentropy_weighted_y_vals)  
# 是Sigmoid交叉熵损失函数 的加权，对正目标加权 
# -\left [weight * t * ln\left ( \frac{1}{1+e^{-x}} \right ) \right ] - \left [ \left ( 1 - t \right ) * ln\left ( 1 - \frac{1}{1+e^{-x}} \right ) \right ]

加权交叉熵损失函数 是 Sigmoid交叉熵损失函数的加权，对正目标进行加权。上述使用过程中，权重是 0.5。
对应公式如下：

这里传入的 targets, x_vals, weight 的参数传入顺序，参考代码时需要注意。

8.Softmax交叉熵损失函数(Softmax cross entropy loss)

unscaled_logits = tf.constant([[1., -3., 10.]])  
target_dist = tf.constant([[0.1, 0.02, 0.88]])  
softmax_xentropy = tf.nn.softmax_cross_entropy_with_logits_v2(labels=unscaled_logits, logits=target_dist)  
print(sess.run(softmax_xentropy))

Softmax交叉熵损失函数可作用于非归一化的输出结果，只针对单个目标分类计算损失,通过 softmax 函数将输出结果转化成概率分布，然后计算真值概率分布的损失。
需要注意，使用时，tf.nn.softmax_cross_entropy_with_logits 已经更换成 tf.nn.softmax_cross_entropy_with_logits_v2。
类似以下公式：

注意 这个方法只针对单个目标分类计算损失。

9.稀疏Softmax 交叉熵损失函数(Sparse softmax cross-entropy loss)

unscaled_logits = tf.constant([[1., -3., 10.]])  
sparse_target_dist = tf.constant([2])  
sparse_xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=unscaled_logits, labels=sparse_target_dist)  
print(sess.run(sparse_xentropy))  
# output is [0.00012564]

稀疏Softmax 交叉熵损失函数，用实数来表示类别，Softmax交叉熵损失函数是使用One-hot二进制码来表示，近似概率分布。

10.几种损失函数对比分析

针对几种不同的损失函数进行对比分析，前面三种在回归算法中常使用的：L1正则损失函数、L2正则损失函数和 Pseudo-Huber 损失函数对比分析如下：

x_array = sess.run(x_vals)
plt.plot(x_array, l2_y_out, 'b-', label='L2 Loss')
plt.plot(x_array, l1_y_out, 'r--', label='L1 Loss')
plt.plot(x_array, phuber1_y_out, 'k-.', label='P-Huber Loss (0.25)')
plt.plot(x_array, phuber2_y_out, 'g:', label='P-Huber Loss (5.0)')
plt.ylim(-0.2, 0.4)  
plt.legend(loc='lower right', prop={'size': 11})
plt.show()  

对比结果如下：

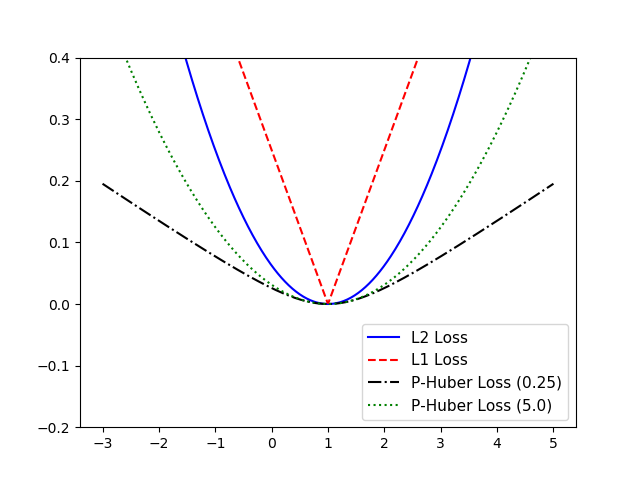
从图中可以看出，Pseudo-Huber 损失函数 传入的delta 参数对于计算损失函数的影响主要体现在平滑程度上。 delta 值越大，计算的loss 越激进。L1正则损失函数在目标值附近确实不是平滑的。
相对来说，L2 更稳定，但缺少健壮，L1正好相反。Pseudo-Huber 损失函数相比起来更健壮和稳定。

针对几种分类算法中常使用的损失函数进行对比分析：Hinge损失函数、两类交叉熵损失函数、Sigmoid交叉熵损失函数和 加权交叉熵损失函数对比分析如下：

x_array = sess.run(x_vals)
plt.plot(x_array, hinge_y_out, 'b-', label='Hinge Loss')
plt.plot(x_array, xentropy_y_out, 'r--', label='Cross-entropy loss')
plt.plot(x_array, xentropy_sigmoid_out, 'k-.', label='Cross-entropy sigmoid loss')
plt.plot(x_array, xentropy_weighted_y_out, 'g:', label='Weighted Cross-entropy loss')
plt.ylim(-1.5, 3)
plt.legend(loc='lower right', prop={'size': 11})
plt.show()  

对比结果如下：

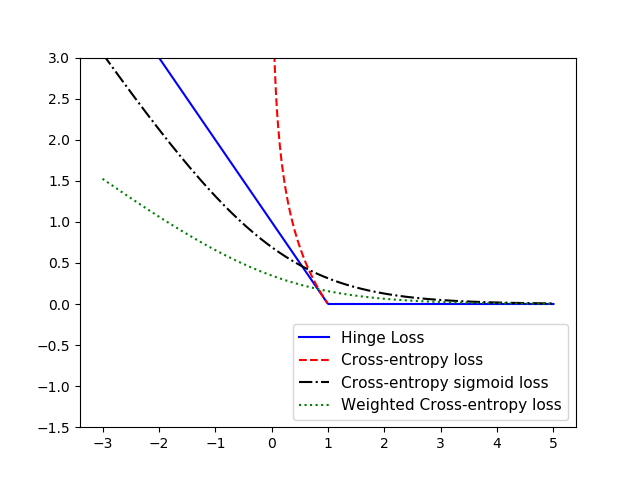
从图中可以直观地看出，Hinge损失函数在 t 不变的情况下，1 - t*x 基本可看作线性的，两类交叉熵损失函数下降速度很快。

以上大多数描述分类算法损失函数都是针对二分类问题，若 想要拓展成多分类，可对 每个预测值 除以 目标 的交叉熵求和进行扩展。

参考资料

• Tensorflow机器学习实战指南
• Tensorflow四种交叉熵函数计算公式
• sparse_softmax_cross_entropy_with_logits 与 softmax_cross_entropy_with_logits 对比
• Tensorflow损失函数总结
• softmax-vs-softmax-loss-numerical-stability